PEMROGRAMAN BERORIENTASI OBJEK

Pengujian jalur dasar

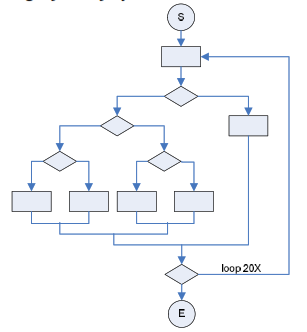
Pengujian jalur dasar merupakan salah satu teknik pengujian kotak putih yang pertama kali diperkenalkan oleh Tom McCabe pada tahun 1976 [2]. Pengujian ini memungkinkan perancangan kasus uji yang diturunkan dari pengukuran tingkat kompleksitas (cyclomatic complexity) struktur program. Ukuran tingkat kompleksitas tersebut menjadi panduan di dalam menentukan jalur-jalur dasar (basis path). Kasus uji yang didapat menjadi kasus uji yang digunakan untuk membuktikan bahwa setiap pernyataan (statement) dari program akan dieksekusi minimal sekali. Pengujian jalur dasar digunakan untuk efisiensi dan efektifitas pengujian kotak putih, karena di dalam pengujian kotak putih tidak mungkin seluruh kemungkinan jalur dieksekusi. Sebagai ilustrasi, jika terdapat sebuah struktur program sebagaimana terdapat pada Gambar 1 dengan 5 kemungkinan jalur untuk setiap loop, maka akan terdapat 5 kemungkinan jalur yang harus diuji [1]. Jika setiap jalur membutuhkan waktu pengujian selama 1 milidetik maka total waktu yang dibutuhkan untuk pengujian sebanyak jalur tersebut adalah 3.170 tahun. Hal ini sangat tidak mungkin ! Oleh karena itu, dibutuhkan sebuah teknik pengujian yang bisa merepresentasikan jalur-jalur pengujian yang ada dengan menggunakan jalur-jalur dasar sebagai jalur ujinya.

Langkah-langkah untuk melakukan pengujian jalur dasar adalah [2] : Menggambarkan grafik alir (flow graph) berdasarkan algoritma perancangan prosedur/fungsi. Menentukan cyclomatic complexity. Menentukan jalur-jalur dasar sesuai dengan jumlah dari cyclomatic complexity. Mendefinisikan kasus-kasus uji untuk setiap jalur dasar yang telah ditentukan. A. Grafik Alir Grafik alir adalah sebuah notasi sederhana yang merepresentasikan aliran kontrol dari sebuah struktur program. Gambar 2 menjelaskan notasi-notasi yang digunakan untuk merepresentasikan jenis-jenis kontrol yang terdapat pada suatu program.

Langkah-langkah untuk melakukan pengujian jalur dasar adalah [2] :

·Menggambarkan grafik alir (flow graph) berdasarkan algoritma perancangan prosedur/fungsi. Menentukan cyclomatic complexity.

·Menentukan jalur-jalur dasar sesuai dengan jumlah dari cyclomatic complexity.

·Mendefinisikan kasus-kasus uji untuk setiap jalur dasar yang telah ditentukan.

A.Grafik Alir

Grafik alir adalah sebuah notasi sederhana yang merepresentasikan aliran kontrol dari sebuah struktur program. Gambar 2 menjelaskan notasi-notasi yang digunakan untuk merepresentasikan jenis-jenis kontrol yang terdapat pada suatu program.

Dalam sebuah grafik alir, anak panah disebut sebagai sisi (edge, E) merepresentasikan aliran kontrol; lingkaran disebut sebagai simpul (node, N) merepresentasikan satu atau lebih aksi/pernyataan lojik; daerah yang dibatasi oleh sisi dan simpul disebut area (region, R); simpul yang mengandung keputusan disebut sebagai predicate node, P yaitu simpul yang mengeluarkan lebih dari satu sisi. Beberapa panduan penting dalam penggambaran sebuah grafik alir adalah [2] :

·Serangkaian aksi/pernyataan lojik dan sebuah pernyataan desisi bisa direpresentasikan dalam sebuah sisi.

·Sebuah sisi harus berakhir pada sebuah simpul, walaupun simpul tersebut tidak merepresentasikan sebuah aksi apapun.

·Penghitungan jumlah area melibatkan sebuah area yang berada di luar grafik alir.

·Desisi majemuk (compound decision), yaitu desisi yang mengandung operator Boolean (AND, OR, NAND dan NOR) tidak boleh direpresentasikan dalam sebuah simpul.

B. Cyclomatic Complexity

Cyclomatic complexity, V(G) adalah sebuah besaran perangkat lunak yang menyatakan ukuran tingkat kompleksitas sebuah program [2]. Angka ini menentukan jumlah jalur dasar yang harus diuji minimal sekali dari sebuah program. Secara matematis, V(G) dapat ditentukan salah satu cara dari beberapa pendekatan berikut :

·V(G) = jumlah area (R)

·V(G) = E - N + 2

·V(G) = P + 1

Berdasarkan studi yang dibuat oleh sejumlah industri, semakin besar nilai V(G) maka semakin besar probabilitas terjadinya kesalahan program

Jalur Dasar

Jalur dasar adalah sebuah jalur pada program yang mengandung paling sedikit sebuah pernyataan lojik [2]. Dalam konteks grafik alir, maka sebuah jalur disebut sebagai jalur dasar jika jalur tersebut memiliki paling tidak satu buah simpul yang belum pernah dilalui oleh jalur yang sudah didefinisikan sebelumnya. Jumlah jalur dasar yang teridentifikasi harus sesuai dengan nilai dari cyclomatic complexity, V(G).

Penentuan Kasus

Uji Kasus uji adalah suatu kondisi yang dibuat untuk menjamin bahwa sebuah jalur dasar dapat diuji. Sebuah kasus uji harus memuat kondisi/data awal, prosedur uji dan hasil yang diharapkan dari sebuah jalur dasar yang akan diuji. Sebuah jalur dasar mungkin tidak bisa diuji secara mandiri, tetapi harus menjadi bagian dari kasus uji jalur dasar yang lain.